Hướng Dẫn Sử Dụng Hàm POWER Trong Excel

Hàm POWER Trong Excel Là Gì?

Hàm POWER trong Excel là một hàm đơn giản giúp bạn nâng một số nào đó lên một lũy thừa. Lũy thừa có thể là một số cố định hoặc một tham chiếu đến bất kỳ ô nào trong bảng tính của bạn. Tham số lũy thừa của hàm POWER có thể là số dương hoặc số âm. Khi sử dụng để biểu diễn ký hiệu khoa học, lũy thừa dương cho phép bạn làm việc với các số lớn, trong khi lũy thừa âm được sử dụng để làm việc với các giá trị nhỏ.

Ngoài từ khóa POWER chuẩn, hàm này còn có một toán tử rút gọn, đó là toán tử mũ (^). Khi sử dụng trong công thức, toán tử mũ sẽ thực hiện cùng một phép tính như hàm POWER. Hàm POWER yêu cầu hai tham số: số bạn muốn nâng lên và lũy thừa bạn muốn nâng nó lên.

Hàm POWER cũng có thể được biểu diễn bằng một chuỗi các phép nhân. Hai công thức sau sẽ cho ra cùng một kết quả:

=POWER(5, 3)

=5*5*5

Việc nhân một số với chính nó nhiều lần sẽ cho ra kết quả giống như hàm POWER hoặc toán tử rút gọn của nó, nhưng trong hầu hết các trường hợp, việc sử dụng hàm sẽ dễ đọc hơn nhiều.

Tham số đầu tiên có thể là bất kỳ số thực nào và có thể được nhập trực tiếp vào hàm hoặc tham chiếu từ bất kỳ đâu trong bảng tính hiện tại. Tham số thứ hai, lũy thừa, có thể là bất kỳ số nguyên thực nào, dương hoặc âm.

Cách Sử Dụng Hàm POWER Trong Excel

Hàm POWER có thể được sử dụng độc lập dưới dạng hàm hoặc toán tử. Nó cũng có thể được lồng vào các hàm khác để tạo ra các công thức toán học phức tạp hơn.

Cú pháp của hàm POWER như sau:

=POWER(number, power)

Trong đó “number” là số gốc và “power” là lũy thừa. Ví dụ, nếu bạn muốn nâng số 2 lên lũy thừa 3, bạn sẽ viết:

=POWER(2,3)

Kết quả của phép tính này sẽ là 8.

=POWER(A2, 2)

Ở đây, bất kỳ số nào được đặt vào ô A2 sẽ được bình phương và kết quả sẽ được trả về bởi hàm. Cùng một hàm có thể được viết dưới dạng rút gọn của hàm POWER:

=A2^2

Khi sử dụng toán tử POWER thay vì hàm, số gốc được đặt ở bên trái của ký hiệu mũ trong khi lũy thừa được đặt ở bên phải.

Sử Dụng Hàm POWER Với Các Lũy Thừa Cố Định Và Tùy Ý

Không chỉ số được nâng lên có thể là tham chiếu đến một ô trong bảng tính hiện tại, mà lũy thừa cũng có thể được truyền qua một ô. Việc truyền lũy thừa qua một ô sẽ tạo ra một hàm như sau:

=POWER(15, A2)

Kết quả của hàm trên sẽ là 15 nâng lên lũy thừa được đặt trong A2. Chúng ta có thể sử dụng một trong các công thức mảng của Excel, các công thức sử dụng một phạm vi tham chiếu ô thay vì một giá trị đơn lẻ như được minh họa dưới đây, để tạo một biểu đồ lũy thừa đơn giản hiển thị danh sách các lũy thừa.

Biểu đồ được tạo bằng một hàm duy nhất:

=POWER(A2:A11, B1:K1)

Đây là một công thức mảng. Nó sử dụng mỗi ô từ A2 đến A11 làm tham số đầu tiên của hàm POWER, và sử dụng mỗi ô từ B1 đến K1 làm tham số thứ hai. Nếu hàm được đặt trong ô B2, thì kết quả sẽ tự động được đặt trong mỗi ô từ B2 đến K11 để tạo ra bảng trên.

Sử Dụng Hàm POWER Trong Các Phép Tính

Mặc dù hàm POWER của Excel có các trường hợp sử dụng hạn chế khi làm việc độc lập, nhưng thú vị là nó hoạt động tốt như một máy tính bình phương đơn giản:

=POWER(A2, 2)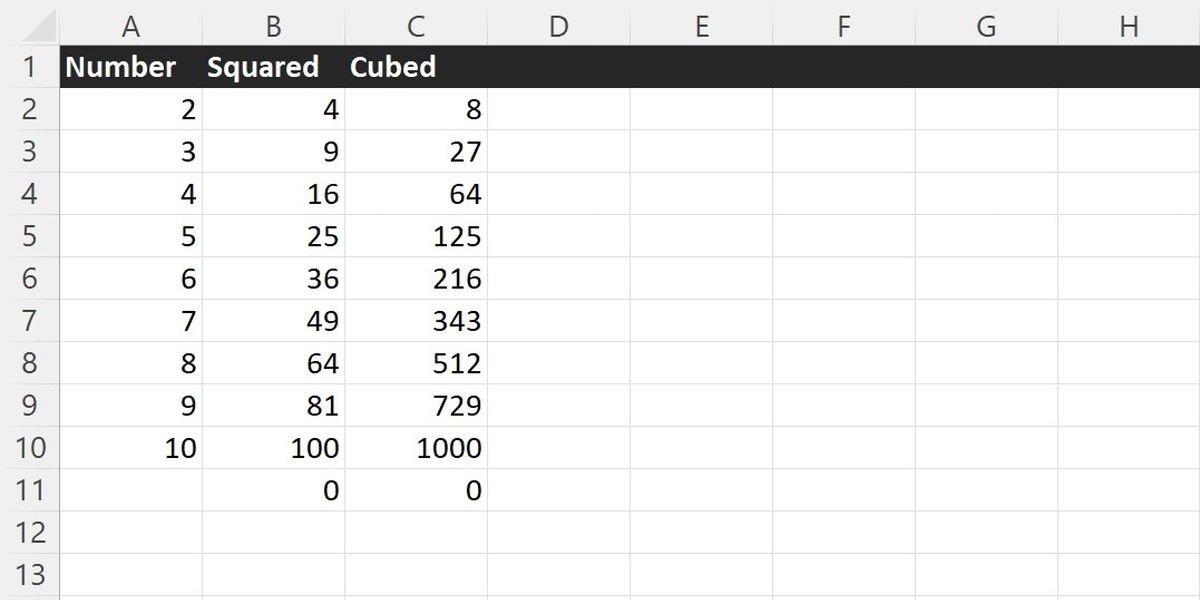

Danh sách các số từ 1 đến 10 trong Excel. Mỗi số đều có giá trị bình phương của nó

Một đặc điểm đáng chú ý trong ví dụ trên là giá trị của B11 và C11. Nếu ô tham chiếu để nâng lên bất kỳ lũy thừa nào là ô trống, nó sẽ được coi là 0. Kết quả của việc chạy hàm POWER trên một ô trống sẽ luôn là 0.

Sử Dụng Hàm POWER Để Tính Diện Tích Hình Tròn Trong Excel

Một trường hợp sử dụng tốt hơn, tuy nhiên, có thể thấy với một chút hình học đơn giản. Bằng cách kết hợp hàm POWER vào một công thức toán học, chúng ta có thể tính diện tích và chu vi của một hình tròn với bán kính thay đổi.

Diện tích của hình tròn bằng PI nhân với bán kính bình phương. Công thức này có thể nhanh chóng được chuyển thành máy tính diện tích trong Excel:

1. Đặt bán kính của các hình tròn bạn muốn tính vào cột A.
2. Hàm POWER có thể được sử dụng để bình phương bán kính bằng cách sử dụng tham chiếu ô làm tham số đầu tiên và 2 làm tham số thứ hai.
3. PI có thể được ước lượng bằng 3.14, hoặc để có phép đo chính xác hơn, bạn có thể sử dụng hàm PI của Excel. Nhân hàm PI với bán kính bình phương.

Sau khi ô đầu tiên, C2 đã được tạo, sử dụng tay cầm kéo ở góc dưới bên phải của ô để điền vào cột.

=PI() * POWER(A2, 2)

Cuối cùng, để dễ đọc, tốt nhất là tránh các số thập phân không cần thiết. Có một vài cách khác nhau để thay đổi số thập phân trong Excel. Trong ví dụ này, hàm ROUND là cách đơn giản nhất.

Hàm ROUND của Excel có thể cắt bớt kết quả đến một số chữ số thập phân cụ thể. Sử dụng công thức từ trên làm tham số đầu tiên cho hàm ROUND, và số chữ số thập phân bạn muốn làm tròn đến làm tham số thứ hai.

=ROUND(PI() * POWER(A2, 2), 2)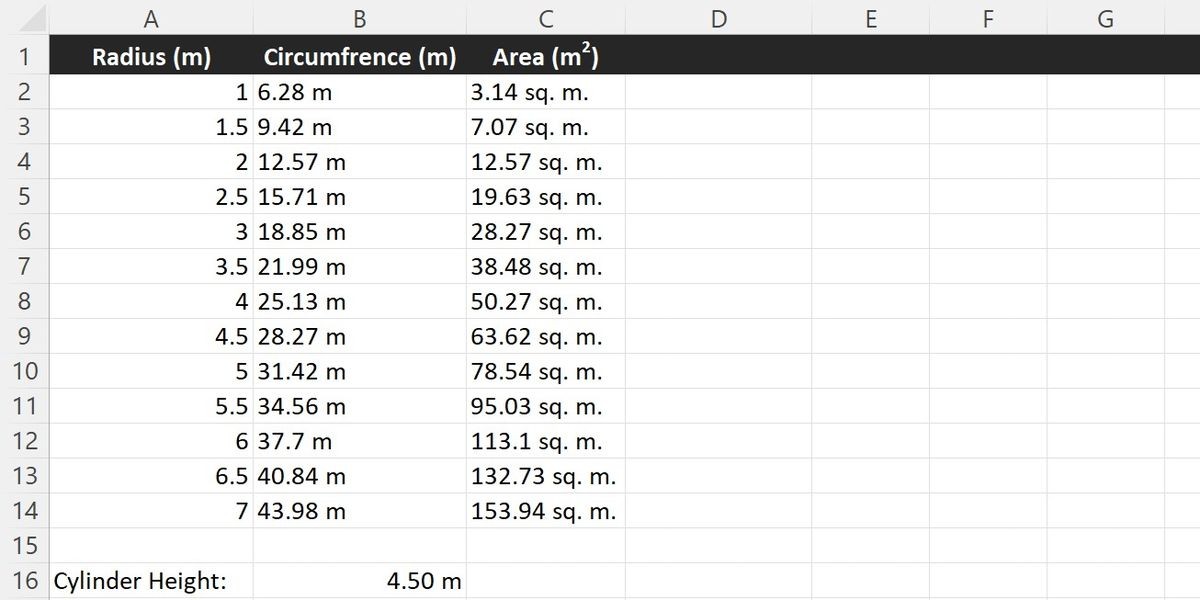

Danh sách bán kính hình tròn với chu vi và diện tích của mỗi hình tròn trong Excel.

Tính Thể Tích Hình Trụ Trong Excel

Thêm một biến số vào phương trình, bạn có thể xác định thể tích sẽ là bao nhiêu cho một hình trụ. Phương trình cho thể tích của hình trụ chỉ đơn giản là phương trình cho diện tích của hình tròn nhân với chiều cao của hình trụ, h.

Trong bảng tính mới, B16 chứa chiều cao của hình trụ. Với một chút thay đổi, chúng ta có thể nhân công thức ban đầu mà chúng ta đã sử dụng để tìm diện tích với chiều cao.

=ROUND(PI() * POWER(A2, 2) * B$16, 2)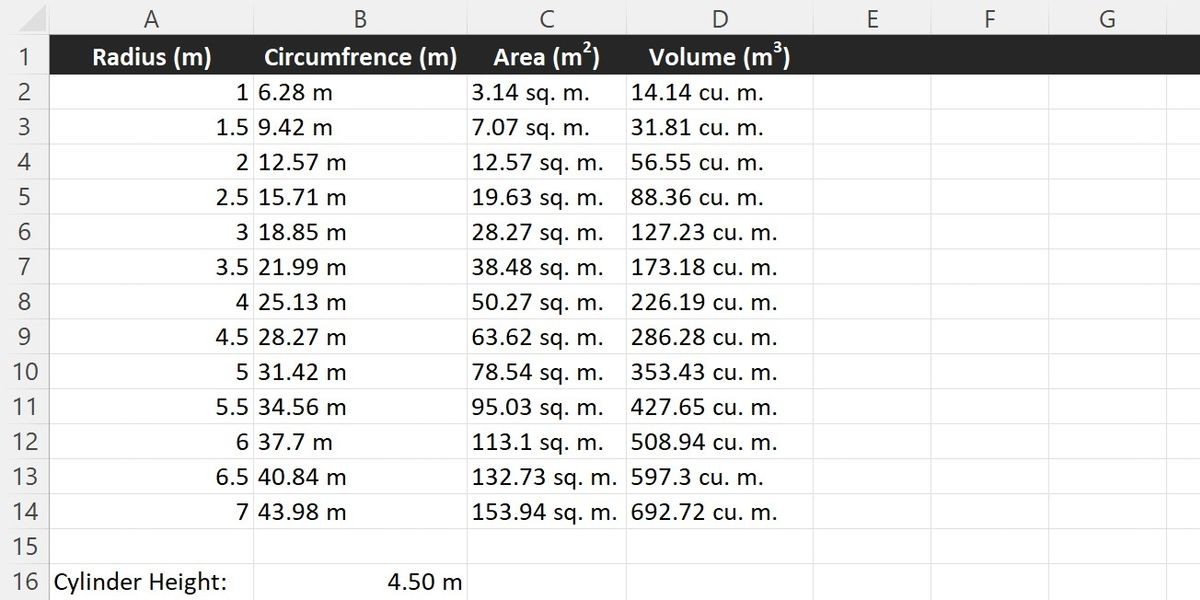

Máy tính trong Excel xác định thể tích của hình trụ khi biết bán kính và chiều cao.

Sử Dụng Hàm POWER Để Xác Định Căn Bậc Tùy Ý Trong Excel

Hàm POWER thường được sử dụng khi tạo các công thức toán học phức tạp để vẽ đồ thị. Việc trực quan hóa các công thức như vậy với các công cụ vẽ đồ thị và biểu đồ tích hợp của Excel là rất dễ dàng.

Một cách khác để sử dụng hàm POWER là tạo một máy tính căn bậc tùy ý. Excel có hàm SQRT tích hợp để tìm căn bậc hai, nhưng đối với căn bậc ba hoặc bất kỳ căn bậc nào lớn hơn 2, bạn sẽ cần thực hiện một số phép tính bổ sung.

Bất kỳ căn bậc nào cũng có thể được tìm thấy bằng cách nâng số đó lên một chia cho số căn bậc. Một máy tính căn bậc ba có thể được tạo bằng cách nâng bất kỳ số nào lên 1/3. Hàm POWER của Excel cho phép bạn nhanh chóng và dễ dàng tìm các căn bậc tùy ý.

Sử dụng một chia cho bất kỳ số nào làm lũy thừa sẽ chuyển hàm POWER thành máy tìm căn bậc cho số đó. Ví dụ, hàm dưới đây sẽ tìm căn bậc ba của số trong A2:

=POWER(A2, 1/3)

Chia một cho bất kỳ số thực nào để tạo một hàm tìm căn bậc tùy ý bằng cách tham chiếu một ô trong bảng tính của bạn làm mẫu số trong tham số thứ hai:

=ROUND(POWER(A2, 1/$B$12), 2)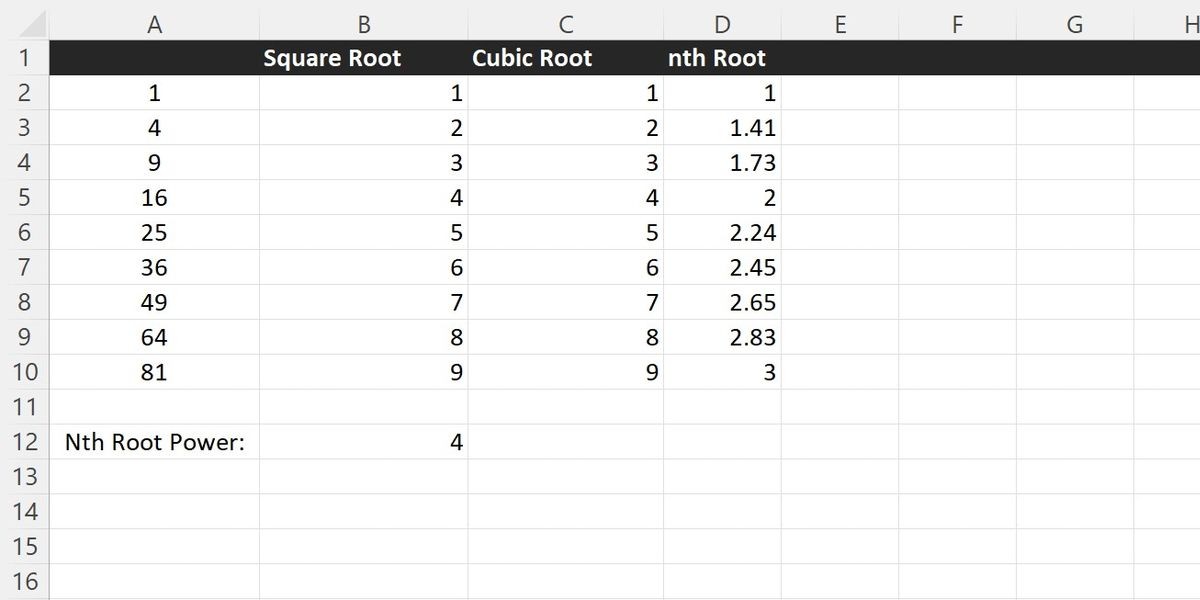

Máy tính trong Excel tìm căn bậc hai, căn bậc ba và một căn bậc tùy ý cho một danh sách các số

Hàm POWER cũng có thể được sử dụng như một cách dễ dàng để hiển thị ký hiệu khoa học. Hiển thị các số của bạn trong ký hiệu khoa học sẽ cho phép bạn làm việc dễ dàng hơn với các giá trị rất lớn hoặc rất nhỏ. Ký hiệu khoa học có thể được tạo dễ dàng bằng cách sử dụng hàm POWER trên 10, và một số dương hoặc một số âm:

=A2 * POWER(10, B2)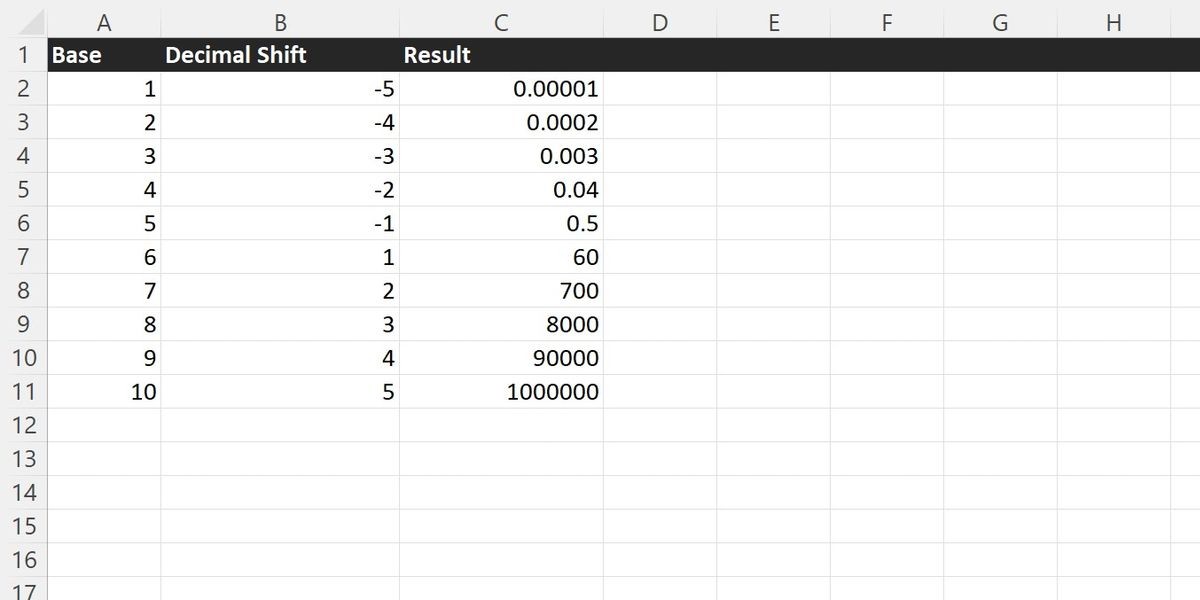

Danh sách các số trong Excel được sử dụng làm cơ sở cho các phép tính khoa học.

Bạn thậm chí có thể sử dụng hàm POWER như một phần của máy tính sử dụng ký hiệu khoa học. Bạn có thể thực hiện các phép tính cơ bản trên các số phức tạp trong khi vẫn giữ chúng ở định dạng dễ đọc:

=SUM(A2 * POWER(10, B2), C2 * POWER(10, D2))

=(A2 * POWER(10, B2)) - (C2 * POWER(10, D2))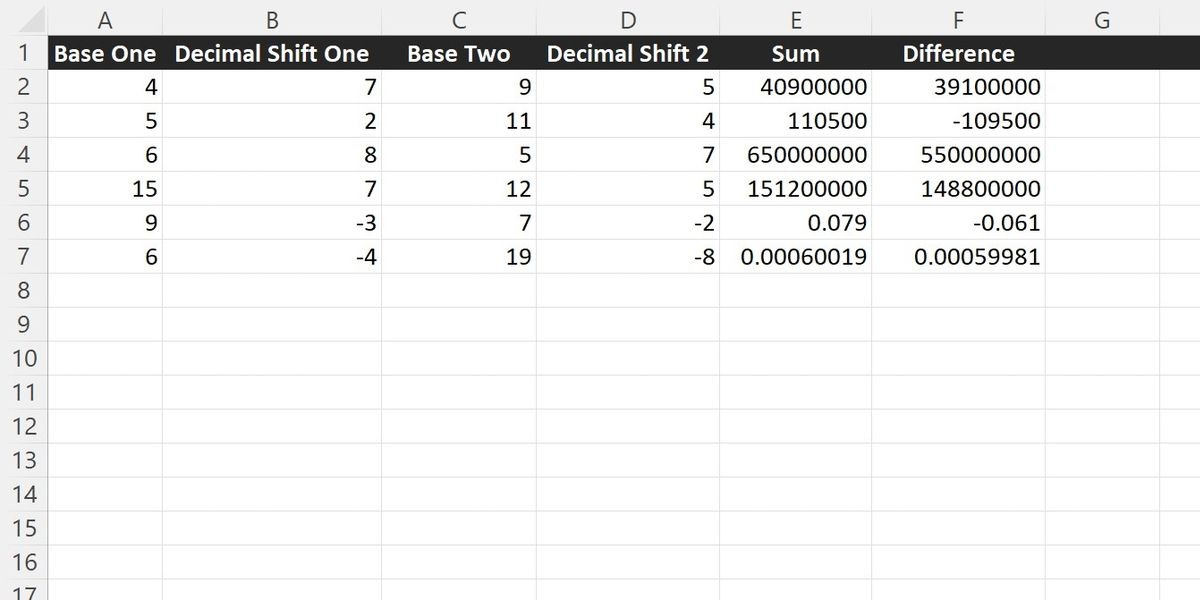

Máy tính trong Excel cộng và trừ các số khác nhau trong ký hiệu khoa học.